03. 에너지 수지(energy balance)

 

• 화학 공정을 설계할 때 가장 중요한 일 중의 하나는 각 화학 공정 장치의 에너지 수지

• 에너지 수지를 계산할 때는 일정한 경계(boundary) 안에 일어나는 변화만을 생각

• 경계 안에 포함된 모든 부분을 계(system, 화공 장치), 그 외의 부분을 주위(surrounding), 주위는 열과 일들을 교환하는 상호 작용

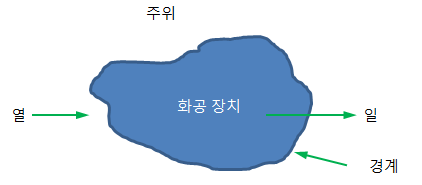
(1) 에너지 수지의 기본 원리

• 장치 중에 출입하는 모든 에너지의 수지 균형을 수량적으로 표시

• 에너지 보존의 법칙을 응용하여 에너지 수지를 계산, 열역학 제1법칙

        

 

(1) 유체 에너지 수지

에너지의 형태

• 운동 에너지(kinetic energy) : 질량이 m(kg)인 유체가 속도 u(m/s)로 운동할 때 나타내는 에너지

        

• 위치 에너지 : 질량이 m(kg)인 유체가 기준면으로부터 높이 h(m)에 있을 때 나타내는 에너지

        

• 압력 에너지(pressure energy) : 질량이 m(kg), 압력이 p(N/m²)에 대응하는 일을 할 때 이일에 해당하는 만큼의 에너지

         

• 기계적 에너지 : 운동 에너지, 위치 에너지, 압력 에너지을 통틀어 기계적 에너지

두(head)

• 단위 질량의 유체가 가지고 있는 에너지, 크기는 길이(m)

• 단위 질량의 에너지를 중력 가속도 g(m/s2)로 나누어 주면, 각 에너지는 액체의 기둥 높이로 나타난다.

• 속도두(velocity head) =
• 위치두(potential head) =

• 압력두(pressure head) =

예제 2-10)

    비중이 0.9인 액체가 나타내는 압력이 2atm일 때 이를 두로 환산하여라.

풀이)

        압력두(pressure head) = 에서

         p = 2atm = (2)(101,325N/m²) = 202,650N/m²

              = 0.9g/cm³ = 900kg/m³

             속도두  =  

예제 2-11)

    기준면에서 3m 높이에 있는 수평관 속에 물이 1m/s로 흐르고 있다. 속도두와 위치두를 계산하여라.

풀이)

    속도두(velocity head) =

    위치두(potential head) =

 

 

1.1.2.3. 유체의 에너지 수지

1.1.2.3.1.1. 비압축성 유체가 그림과 같은 관을 통하여 정상 상태로 흐른다고 가정

1.1.2.3.1.1.1. 기준면에서 의 높이에 있는 단면 ①, ②에서 유속을 , 압력을 , 밀도

1.1.2.3.1.1.2. 단면 ①, ②에서 단위 질량의 유체를 펌프 또는 송풍기로 수송하는데 필요한 에너지

1.1.2.3.1.1.3. 마찰 손실(friction loss) 등에 의하여 손실되는 에너지

1.1.2.3.1.1.4. 유체가 단면 ①에서 가지고 있는 에너지에 ①~②에서 얻은 에너지를 합한 것은 단면 ②로부터 가지고 나온 에너지에 ①~②에서 잃은 에너지 손실(두손실)를 합한 것과 같다.

1.1.2.3.1.1.5. 유체 1kg에 대하여 ①~② 구간의 기계적 에너지 수지식은

1.1.2.3.1.1.6. 기계적 에너지 수지식은 단면 ①과 단면 ②의 유체의 내부 에너지가 같고, 축일 는 유체가 외부에 하는 일인데, 펌프의 일은 외부에서 계에 가하는 에너지이므로 방향이 서로 반대

1.1.2.3.1.1.7. 열 는 외부에서 가해 주는 것이지만 마찰 손실 는 마찰에 의해 생긴 열에너지가 외부로 나가므로 방향이 반대

1.1.2.3.1.1.8. 유체가 비압축성이고 단면 ①~② 구간에 펌프 및 마찰 손실 등이 없을 때에 이 되므로 기계적 에너지 수지식은 속도두, 위치두, 압력두의 합이 일정하므로 이 식을 베르누이의 정리(Bernoulli's therorem), 각 항의 차원은 (에너지/질량)으로서 유체의 단위 질량에 대한 에너지를 나타내고 표준 단위는

1.1.2.3.1.1.9. 유체 1kg에 주어지는 펌프의 에너지 량은

1.1.2.3.1.1.10. 유체 1kg을 단면 ①에서 단면 ②로 보내는 데 필요한 에너지(펌프 등에 의한 일)를 라 하고 유량을 라 하면 동력 는

1.1.2.3.1.1.11. 펌프의 효율을 라 하면 펌프가 필요로 하는 에너지(일), 는 유체 수송에 소요되는 에너지 는

1.1.2.3.1.1.12. 유체 수송을 위한 펌프가 사용한 동력

예제 2-12) 그림과 같이 물을 퍼올리는 장치에서 비중이 1.05인 용액을 위의 탱크에 올리려고 한다. 흡입관과 배출관의 안지름을 각각 90mm, 60mm, 흡입관의 평균 유속을 1.20m/s, 흡입 액면에서 펌프의 중심까지의 높이, 즉흡입 양정은 2m, 펌프로부터 배출되는 액면까지의 높이, 즉 배출 양정은 20m이다. 펌프의 출력은 4.5PS, 효율은 62%이다. 이 수송관 안의 마찰 손실은 얼마나 되겠는가?

풀이)

단면 ①~②에서 에너지 수지를 취하면

질량 유속 은

펌프가 용액에 주는 에너지는

W =	P	=	0.62	4.5PS	735.5W	=259.1J/kg
			8.01kg/s		1PS

, 탱크는 용량이 크므로

배출관에서의 유속 는 흡입관에서의 유속 으로부터 연속의 식에 의해

이들 값을 위의 식에 대입하면